| Design of Control System for Abstract System on Banach lattice |
 |
|
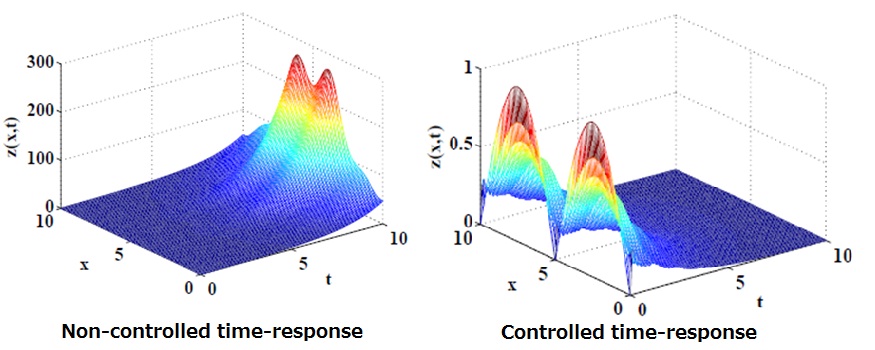
Partial differential equations and delay differential equations are known to be infinite-dimensional systems, while ordinary differential equations are finite-dimensional systems. The control of infinite-dimensional systems is a challenging problem attracting considerable attention in many research fields. Semigroups have become important tools in infinite-dimensional control theory over the past several decades. The semigroup method is a unified approach to addressing systems that include ordinary differential equations, partial differential equations, and delay differential equations. The behaviors of many dynamical systems including infinite-dimensional systems and finite-dimensional systems can be characterized by the semigroup theory. Using the semigroup theory, we introduce the concept of an abstract system that can be used to characterize the behavior of a wide class of mathematical models. We examine the stabilization problem of an abstract system on a Banach lattice using the semigroup theory. To tackle this problem, we take advantage of the properties of a nonnegative semigroup on a Banach lattice. The objective of this study is to propose a stabilization method for an abstract system on a Banach lattice. In many systems arising from physics, biology, chemistry, and economics, a solution with a nonnegative initial value should remain nonnegative. An illustrative example is shown here. The growth of virus population can be described by a partial differential equation with time delay and its solution satisfies the nonnegativity. The left figure shows that the virus population is increasing without control input. On the other hand, the right figure shows that the extinction of viruses can be achieved by employing control inputs. This research is partially supported by the Telecommunications Advancement Foundation and the Ministry of Education, Culture, Sports, Science and Technology, Grant-in-Aid for Young Scientists (B), 22760318. [References]
|